dayana

TEMA: SIGNIFICADO Y USO DE LAS LITERALES

Subtema: Ecuaciones

Una ecuación de primer grado es aquella en la cual el máximo esponente de las incógnitas es 1.

Dos ecuaciones de primer grado con dos incógnitas son un sistema de ecuaciones con dos incógnitas. Por ejemplo:

x+y= 36
6x+8y=258

Los valores de x y Y son solución de ambas ecuaciones son la solución del sistema.

Resolver una ecuación consiste en hallar los valores de la variable que hacen cierta la igualdad.

MÉTODO GRÁFICO

*Se despeja una incógnita en una de las ecuaciones.

* Se sustituye la expresión de esta incógnita en la otra ecuación, obteniendo un ecuación con una sola incógnita.

* Se resuelve la ecuación.

* El valor obtenido se sustituye en la ecuación en la que aparecía la incógnita despejada.

*Los dos valores obtenidos constituyen la solución del sistema.

MÉTODO DE IGUALACIÓN

Consiste en una pequeña variante del antes visto de sustitución. Para resolver un sistema de ecuaciones por este método hay que despejar una incógnita, la misma, en las dos ecuaciones e igualar el resultado de ambos despejes, con lo que se obtiene una ecuación de primer grado.

Pasos para resolver una ecuación por éste método:

Se despeja la misma incógnita en ambas ecuaciones.
Se igualan las expresiones obtenidas y se resuelve la ecuación lineal de una incógnita que resulta.
Se calcula el valor de la otra incógnita sustituyendo la ya hallada en una de las ecuaciones despejadas de primer paso.

EJEMPLO:

Entre Ana y Sergio tienen 600 euros, pero Sergio tiene el doble de euros que Ana. ¿Cuánto dinero tiene cada uno?.

Llamemos x al número de euros de Ana e y al de Sergio. Vamos a expresar las condiciones del problema mediante ecuaciones: Si los dos tienen 600 euros, esto nos proporciona la ecuación x + y = 600. Si Sergio tiene el doble de euros que Ana, tendremos que y = 2x. Ambas ecuaciones juntas forman el siguiente sistema:


x + y = 600
   y = 2x

Vamos a resolver el sistema por el método de igualación y ya que en la 2ª ecuación hay una incógnita, la y, despejada, vamos a despejar la misma incógnita en la otra ecuación, con lo que tendremos:

y = 2x
⇒ 2x = 600 - x ⇒ 2x + x = 600 ⇒ 3x = 600 ⇒ x = 600/3 = 200
y = 600 - x

Ahora sustituimos x = 200 en una de las ecuaciones en las que estaba despejada la y, con lo que tendremos:


y = 2x ⇒ y = 400

Por tanto, la solución al problema planteado es que Ana tiene 200 euros y Sergio tiene 400 euros, es decir, el mismo resultado, evidentemente, que habíamos obtenido con el método de sustitución.

MÉTODO DE SUSTITUCIÓN

Consiste en despejar una incógnita en una de las ecuaciones y sustituirla en la otra; así, se obtiene una sola ecuación con una incógnita. Una vez obtenido el valor de esta incógnita, se sustituye su valor en cualquiera de las ecuaciones del sistema, inicial para calcular el valor de la otra incógnita.

Lo que debemos hacer:

1.- Despejar una de las incógnitas en una de las ecuaciones.

2.- Sustituir la expresión obtenida en la otra ecuación.

3.- Resolver la ecuación resultante.

4.- Calcular la otra incógnita en la ecuación despejada.

EJEMPLO:

Resolver
sistemas_ecuaciones004

Se despeja x en la segunda ecuación:
x = 8 – 2y
Se sustituyen en la primera ecuación:
3(8 – 2y) – 4y = – 6
Operando:
24 − 6y − 4y = − 6
24 – 10y = – 6
− 10y = − 6 − 24
− 10y = − 30
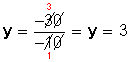
sistemas-ecuaciones005

Se resuelve:
y = 3
Se sustituye este valor en la segunda:
x + 2(3) = 8
x + 6 = 8
x = 8 – 6 = 2
Solución del sistema:
x = 2, y = 3

MÉTODO DE REDUCCIÓN

Pasos para resolver una ecuación por el método de reducción:

Se multiplican o dividen los miembros de las dos ecuaciones por los números que convengan para que una de las incógnitas tenga el mismo coeficiente en ambas.

Se restan las dos ecuaciones resultantes, con lo que se elimina una incógnita.

Se resuelve la ecuación con una incógnita obtenida, y se sustituye su valor en cualquiera de las ecuaciones iniciales para calcular la segunda.

Por ejemplo, en el sistema de ecuaciones: